Compressive Sampling of Ensembles of Correlated Signals

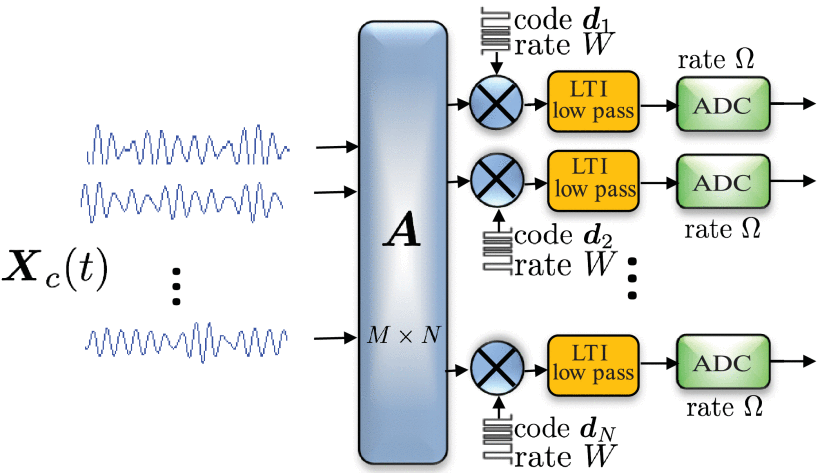
The recently developed theory of Compressive sensing (CS) has shown that sparse signals can be reconstructed from a much smaller number of measurements than their bandwidth suggests. In this paper we present a sampling scheme to acquire ensembles of correlated signals at a sub-Nyquist rate. The sampling architecture uses simple analog building blocks including analog vector matrix multiplier (AVMM) and linear time invariant (LTI) random filters to analog preprocess the signals before sampling them with non-uniform Analog-to-digital converters (ADCs). The sampling strategy takes advantage of the (a priori unknown) correlation structure in the ensemble to sample at a sub-Nyquist rate and stably recover the information using convex optimization. We close the discussion with some applications.