Compressive Multiplexing of Correlated Signals
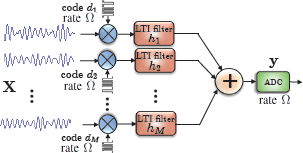
We propose two compressive multiplexers for the efficient sampling of ensembles of correlated signals. We show that we can acquire correlated ensembles, taking advantage of their (a priori-unknown) correlation structure, at a sub-Nyquist rate using simple modulation and filtering architectures. We recast the reconstruction of the ensemble as a low-rank matrix recovery problem from generalized linear measurements. Our theoretical results indicate that we can recover an ensemble of M correlated signals composed of R \ll M independent signals, each bandlimited to W/2 Hz, by taking O(RW log^q W) samples per second, where q > 1 is a small constant.