Blind Deconvolution Using Convex Programming

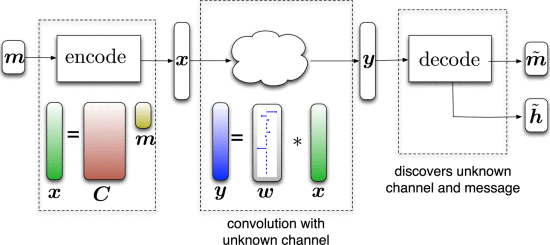
We consider the problem of recovering two unknown vectors, w and x, of length L from their circular convolution. We make the structural assumption that the two vectors are members of known subspaces, one with dimension N and the other with dimension K. Although the observed convolution is nonlinear in both w and x, it is linear in the rank-1 matrix formed by their outer product wx^*. This observation allows us to recast the deconvolution problem as low-rank matrix recovery problem from linear measurements, whose natural convex relaxation is a nuclear norm minimization program. We prove the effectiveness of this relaxation by showing that, for “generic” signals, the program can deconvolve w and x exactly when the maximum of N and K is almost on the order of L. That is, we show that if x is drawn from a random subspace of dimension N, and w is a vector in a subspace of dimension K whose basis vectors are spread out in the frequency domain, then nuclear norm minimization recovers wx^* without error. We discuss this result in the context of blind channel estimation in communications. If we have a message of length N, which we code using a random L \times N coding matrix, and the encoded message travels through an unknown linear time-invariant channel of maximum length K, then the receiver can recover both the channel response and the message when L \geq N + K, to within constant and log factors.