A convex approach to blind deconvolution with diverse inputs
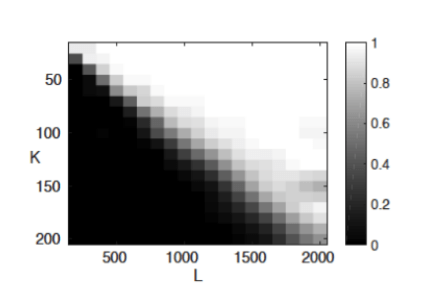
This note considers the problem of blind identification of a linear, time-invariant (LTI) system when the input signals are unknown, but belong to sufficiently diverse, known subspaces. This problem can be recast as the recovery of a rank-1 matrix, and is effectively relaxed using a semidefinite program (SDP). We show that exact recovery of both the unknown impulse response, and the unknown inputs, occurs when the following conditions are met: (1) the impulse response function is spread in the Fourier domain, and (2) the N input vectors belong to generic, known subspaces of dimension K in ℝL. Recent results in the well-understood area of low-rank recovery from underdetermined linear measurements can be adapted to show that exact recovery occurs with high probablility (on the genericity of the subspaces) provided that K,L, and N obey the information-theoretic scalings, namely L \geq K and N \geq 1 up to log factors.